

However, most stars even in our own galaxy are much further away than 1000 parsecs, since the Milky Way is about 30,000 parsecs across. Space based telescopes can get accuracy to 0.001, which has increased the number of stars whose distance could be measured with this method. This limits Earth based telescopes to measuring the distances to stars about 1/0.01 or 100 parsecs away. Parallax angles of less than 0.01 arcsec are very difficult to measure from Earth because of the effects of the Earth's atmosphere. Limitations of Distance Measurement Using Stellar Parallax This simple relationship is why many astronomers prefer to measure distances in parsecs. The lower diagram shows an equal angle swept by the Sun in a geostatic model. In the upper diagram, the Earth in its orbit sweeps the parallax angle subtended on the Sun. The distance d is measured in parsecs and the parallax angle p is measured in arcseconds. Parallax is an angle subtended by a line on a point.
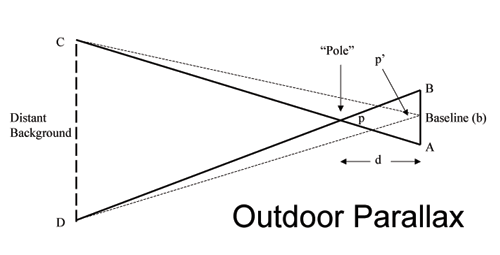
There is a simple relationship between a star's distance and its parallax angle: d = 1/ p Stellar parallax diagram, showing how the 'nearby' star appears to move against the distant 'fixed' stars when Earth is at different positions in its orbit around the Sun. The star's apparent motion is called stellar parallax. Astronomers can measure a star's position once, and then again 6 months later and calculate the apparent change in position. In light-years, it calculates the distance to a nearby star from its stellar parallax in arc seconds and parsecs it. Degrees of difference in parallax angles seen in relation to different distances. Once the distance to the star is known, the stellar parallax angle can be calculated using the following formula: angle (1/distance) (206265/parallax) where parallax is the star’s parallax, in arcseconds. As the Earth orbits the Sun, a nearby star will appear to move against the more distant background stars. Parallax is a trigonometric tool that astronomers use to measure. This effect can be used to measure the distances to nearby stars. Your hand will appear to move against the background. Because the scientists know the distance the Earth has traveled in six months (twice the distance to the Sun), they have all the information they need to find the distance to the star.Another way to see how this effect works is to hold your hand out in front of you and look at it with your left eye closed, then your right eye closed. The angle these astronomers measure the star to move is actually the same angle they would see the Earth move if they could travel to the star. Your eyes model the different positions the Earth is in, first on one side of the Sun (your nose), then the other.Īstronomers look at the sky on a specific date, and then six months later, to see how far a nearby star appears to move relative to the background. Parallax of the Moon, viewed from opposite sides of Earth. Note that if you can measure the parallax angle, and you Moon 2 Earth d b O1 O2 Celestial Sphere M2 M1 Fig. Notice how it shifts position, yet the your thumb hasn't actually moved. where is the parallax angle in degrees, b is the baseline (in this case the diameter of Earth), and d is the distance from the center of Earth to the center of the Moon. Recently, an innovative parametrization (Parallax Angle) has shown to outperform the others in the context of a Bundle. Best way to see this by holding a thumb at arm's length relative to some background (a painting in the wall a chair in front of you whatever works) and look at it through one eye, then the other. Luckily you have your trusty compass and some knowledge about parallax and triangles For the first vantage point, you start with the lighthouse directly north of you. You can see this effect driving in the country.

Because of this, nearby stars will seem to move relative to distant, "background" stars. The parallax angle is defined as one half of the apparent angular motion of the star as Earth orbits from one side of the sun to the opposite side. times the parallax angle subtended by the two observers from the host star. The parallax angle is defined to be one-half of the angle between the projected locations of. The distance d is measured in parsecs and the parallax angle p is measured in arcseconds. To gain experience in measuring angles and distances. The Earth revolves around the Sun every year, so that every half year (six months) it is on the opposite side of the sun from where it was six months ago. Position angles and coplanarity of multiple systems from transit timing. There is a simple relationship between a stars distance and its parallax angle: d 1/p.


 0 kommentar(er)
0 kommentar(er)
